Basic graphics

Introduction

The path module allows one to construct PostScript-like paths, which are one of the main building blocks for the generation of drawings. A PostScript path is an arbitrary shape consisting of straight lines, arc segments and cubic Bézier curves. Such a path does not have to be connected but may also comprise several disconnected segments, which will be called subpaths in the following.

Todo

example for paths and subpaths (figure)

Usually, a path is constructed by passing a list of the path primitives moveto, lineto, curveto, etc., to the constructor of the path class. The following code snippet, for instance, defines a path p that consists of a straight line from the point \((0, 0)\) to the point \((1, 1)\)

from pyx import *
p = path.path(path.moveto(0, 0), path.lineto(1, 1))

Equivalently, one can also use the predefined path subclass line and write

p = path.line(0, 0, 1, 1)

While already some geometrical operations can be performed with this path (see next section), another PyX object is needed in order to actually being able to draw the path, namely an instance of the canvas class. By convention, we use the name c for this instance:

c = canvas.canvas()

In order to draw the path on the canvas, we use the stroke() method of the canvas class, i.e.,

c.stroke(p)
c.writeEPSfile("line")

To complete the example, we have added a writeEPSfile() call, which writes the contents of the canvas to the file line.eps. Note that an extension .eps is added automatically, if not already present in the given filename. Similarly, if you want to generate a PDF or SVG file instead, use

c.writePDFfile("line")

or

c.writeSVGfile(“line”)

As a second example, let us define a path which consists of more than one subpath:

cross = path.path(path.moveto(0, 0), path.rlineto(1, 1),
                  path.moveto(1, 0), path.rlineto(-1, 1))

The first subpath is again a straight line from \((0, 0)\) to \((1, 1)\), with the only difference that we now have used the rlineto class, whose arguments count relative from the last point in the path. The second moveto instance opens a new subpath starting at the point \((1, 0)\) and ending at \((0, 1)\). Note that although both lines intersect at the point \((1/2, 1/2)\), they count as disconnected subpaths. The general rule is that each occurrence of a moveto instance opens a new subpath. This means that if one wants to draw a rectangle, one should not use

rect1 = path.path(path.moveto(0, 0), path.lineto(0, 1),
                  path.moveto(0, 1), path.lineto(1, 1),
                  path.moveto(1, 1), path.lineto(1, 0),
                  path.moveto(1, 0), path.lineto(0, 0))

which would construct a rectangle out of four disconnected subpaths (see Fig. Rectangle example a). In a better solution (see Fig. Rectangle example b), the pen is not lifted between the first and the last point:

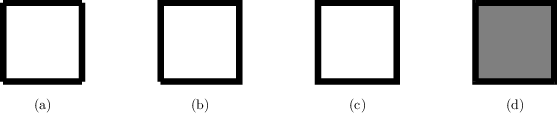
Rectangle example

Rectangle consisting of (a) four separate lines, (b) one open path, and (c) one closed path. (d) Filling a path always closes it automatically.

rect2 = path.path(path.moveto(0, 0), path.lineto(0, 1),
                  path.lineto(1, 1), path.lineto(1, 0),
                  path.lineto(0, 0))

However, as one can see in the lower left corner of Fig. Rectangle example b, the rectangle is still incomplete. It needs to be closed, which can be done explicitly by using for the last straight line of the rectangle (from the point \((0, 1)\) back to the origin at \((0, 0)\)) the closepath directive:

rect3 = path.path(path.moveto(0, 0), path.lineto(0, 1),
                  path.lineto(1, 1), path.lineto(1, 0),
                  path.closepath())

The closepath directive adds a straight line from the current point to the first point of the current subpath and furthermore closes the sub path, i.e., it joins the beginning and the end of the line segment. This results in the intended rectangle shown in Fig. Rectangle example c. Note that filling the path implicitly closes every open subpath, as is shown for a single subpath in Fig. Rectangle example d), which results from

c.stroke(rect2, [deco.filled([color.grey(0.5)])])

Here, we supply as second argument of the stroke() method a list which in the present case only consists of a single element, namely the so called decorator deco.filled. As its name says, this decorator specifies that the path is not only being stroked but also filled with the given color. More information about decorators, styles and other attributes which can be passed as elements of the list can be found in Sect. Attributes: Styles and Decorations. More details on the available path elements can be found in Sect. Path elements.

To conclude this section, we should not forget to mention that rectangles are, of course, predefined in PyX, so above we could have as well written

rect2 = path.rect(0, 0, 1, 1)

Here, the first two arguments specify the origin of the rectangle while the second two arguments define its width and height, respectively. For more details on the predefined paths, we refer the reader to Sect. Predefined paths.

Path operations

Often, one wants to perform geometrical operations with a path before placing it on a canvas by stroking or filling it. For instance, one might want to intersect one path with another one, split the paths at the intersection points, and then join the segments together in a new way. PyX supports such tasks by means of a number of path methods, which we will introduce in the following.

Suppose you want to draw the radii to the intersection points of a circle with a straight line. This task can be done using the following code which results in Fig. Example: Intersection of circle with line yielding two radii

from pyx import *

c = canvas.canvas()

circle = path.circle(0, 0, 2)
line = path.line(-3, 1, 3, 2)
c.stroke(circle, [style.linewidth.Thick])
c.stroke(line, [style.linewidth.Thick])

isects_circle, isects_line = circle.intersect(line)
for isect in isects_circle:
    isectx, isecty = circle.at(isect)
    c.stroke(path.line(0, 0, isectx, isecty))

c.writePDFfile()

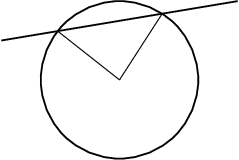
Example: Intersection of circle with line yielding two radii

Here, the basic elements, a circle around the point \((0, 0)\) with radius \(2\) and a straight line, are defined. Then, passing the line, to the intersect() method of circle, we obtain a tuple of parameter values of the intersection points. The first element of the tuple is a list of parameter values for the path whose intersect() method has been called, the second element is the corresponding list for the path passed as argument to this method. In the present example, we only need one list of parameter values, namely isects_circle. Using the at() path method to obtain the point corresponding to the parameter value, we draw the radii for the different intersection points.

Another powerful feature of PyX is its ability to split paths at a given set of parameters. For instance, in order to fill in the previous example the segment of the circle delimited by the straight line (cf. Fig. Example: Intersection of circle with line yielding radii and circle segment), one first has to construct a path corresponding to the outline of this segment. The following code snippet yields this segment

arc1, arc2 = circle.split(isects_circle)
if arc1.arclen() < arc2.arclen():
    arc = arc1
else:
    arc = arc2

isects_line.sort()
line1, line2, line3 = line.split(isects_line)

segment = line2 << arc

Example: Intersection of circle with line yielding radii and circle segment

Here, we first split the circle using the split() method passing the list of parameters obtained above. Since the circle is closed, this yields two arc segments. We then use the arclen(), which returns the arc length of the path, to find the shorter of the two arcs. Before splitting the line, we have to take into account that the split() method only accepts a sorted list of parameters. Finally, we join the straight line and the arc segment. For this, we make use of the << operator, which not only adds the paths (which could be done using line2 + arc), but also joins the last subpath of line2 and the first one of arc. Thus, segment consists of only a single subpath and filling works as expected.

An important issue when operating on paths is the parametrisation used. Internally, PyX uses a parametrisation which uses an interval of length \(1\) for each path element of a path. For instance, for a simple straight line, the possible parameter values range from \(0\) to \(1\), corresponding to the first and last point, respectively, of the line. Appending another straight line, would extend this range to a maximal value of \(2\).

However, the situation becomes more complicated if more complex objects like a circle are involved. Then, one could be tempted to assume that again the parameter value ranges from \(0\) to \(1\), because the predefined circle consists just of one arc together with a closepath element. However, this is not the case: the actual range is much larger. The reason for this behaviour lies in the internal path handling of PyX: Before performing any non-trivial geometrical operation on a path, it will automatically be converted into an instance of the normpath class (see also Sect. path.normpath). These so generated paths are already separated in their subpaths and only contain straight lines and Bézier curve segments. XXX explain normpathparams and things like p.begin(), p.end()-1,

A more geometrical way of accessing a point on the path is to use the arc length of the path segment from the first point of the path to the given point. Thus, all PyX path methods that accept a parameter value also allow the user to pass an arc length. For instance,

from math import pi

r = 2
pt1 = path.circle(0, 0, r).at(r*pi)
pt2 = path.circle(0, 0, r).at(r*3*pi/2)

c.stroke(path.path(path.moveto(*pt1), path.lineto(*pt2)))

will draw a straight line from a point at angle \(180\) degrees (in radians \(\pi\)) to another point at angle \(270\) degrees (in radians \(3\pi/2\)) on a circle with radius \(r=2\). Note however, that the mapping from an arc length to a point is in general discontinuous at the beginning and the end of a subpath, and thus PyX does not guarantee any particular result for this boundary case.

More information on the available path methods can be found in Sect. Class path — PostScript-like paths.

Attributes: Styles and Decorations

Attributes define properties of a given object when it is being used. Typically, there are different kinds of attributes which are usually orthogonal to each other, while for one type of attribute, several choices are possible. An example is the stroking of a path. There, linewidth and linestyle are different kind of attributes. The linewidth might be thin, normal, thick, etc., and the linestyle might be solid, dashed etc.

Attributes always occur in lists passed as an optional keyword argument to a method or a function. Usually, attributes are the first keyword argument, so one can just pass the list without specifying the keyword. Again, for the path example, a typical call looks like

c.stroke(path, [style.linewidth.Thick, style.linestyle.dashed])

Here, we also encounter another feature of PyX’s attribute system. For many attributes useful default values are stored as member variables of the actual attribute. For instance, style.linewidth.Thick is equivalent to style.linewidth(0.04, type="w", unit="cm"), that is \(0.04\) width cm (see Sect. Module unit for more information about PyX’s unit system).

Another important feature of PyX attributes is what is call attributed merging. A trivial example is the following:

# the following two lines are equivalent
c.stroke(path, [style.linewidth.Thick, style.linewidth.thin])
c.stroke(path, [style.linewidth.thin])

Here, the style.linewidth.thin attribute overrides the preceding style.linewidth.Thick declaration. This is especially important in more complex cases where PyX defines default attributes for a certain operation. When calling the corresponding methods with an attribute list, this list is appended to the list of defaults. This way, the user can easily override certain defaults, while leaving the other default values intact. In addition, every attribute kind defines a special clear attribute, which allows to selectively delete a default value. For path stroking this looks like

# the following two lines are equivalent
c.stroke(path, [style.linewidth.Thick, style.linewidth.clear])
c.stroke(path)

The clear attribute is also provided by the base classes of the various styles. For instance, style.strokestyle.clear clears all strokestyle subclasses i.e. style.linewidth and style.linestyle. Since all attributes derive from attr.attr, you can remove all defaults using attr.clear. An overview over the most important attribute types provided by PyX is given in the following table.

Attribute category	description	examples
deco.deco	decorator specifying the way the path is drawn	deco.stroked, deco.filled, deco.arrow, deco.text
style.strokestyle	style used for path stroking	style.linecap, style.linejoin, style.miterlimit, style.dash, style.linestyle, style.linewidth, color.color
style.fillstyle	style used for path filling	color.color, pattern.pattern
style.filltype	type of path filling	style.fillrule.nonzero_winding (default), style.fillrule.even_odd
deformer.deformer	operations changing the shape of the path	deformer.cycloid, deformer.smoothed
text.textattr	attributes used for typesetting	text.halign, text.valign, text.mathmode, text.phantom, text.size, text.parbox
trafo.trafo	transformations applied when drawing object	trafo.mirror, trafo.rotate, trafo.scale, trafo.slant, trafo.translate

Todo

specify which classes in the table are in fact instances

Note that operations usually allow for certain attribute categories only. For example when stroking a path, text attributes are not allowed, while stroke attributes and decorators are. Some attributes might belong to several attribute categories like colours, which are both, stroke and fill attributes.

Last, we discuss another important feature of PyX’s attribute system. In order to allow the easy customisation of predefined attributes, it is possible to create a modified attribute by calling of an attribute instance, thereby specifying new parameters. A typical example is to modify the way a path is stroked or filled by constructing appropriate deco.stroked or deco.filled instances. For instance, the code

c.stroke(path, [deco.filled([color.rgb.green])])

draws a path filled in green with a black outline. Here, deco.filled is already an instance which is modified to fill with the given color. Note that an equivalent version would be

c.draw(path, [deco.stroked, deco.filled([color.rgb.green])])

In particular, you can see that deco.stroked is already an attribute instance, since otherwise you were not allowed to pass it as a parameter to the draw method. Another example where the modification of a decorator is useful are arrows. For instance, the following code draws an arrow head with a more acute angle (compared to the default value of \(45\) degrees):

c.stroke(path, [deco.earrow(angle=30)])

Todo

changeable attributes